どうも、迷える医学生しらいです。
よくネットでは
「高校物理レベルで微分積分を使うのは不毛だ!!」
「そんなことない!難関大では微積が背景の問題がたくさん出ている!」
「微積物理こそが物理の本質だ!!」
「高校物理ごときで本質を語るな!!」
…
などといった議論が延々とかわされる, 未だにホットな話題,
高校物理で微分積分を用いるか論争
今回はそんな微積物理をテーマに記事を書いていこうと思います。
今までにもたくさん微積物理に関する記事を書いてきましたが, この記事は総集編です。
具体的な勉強法などは別の記事で詳述するとして, この記事では私の微積物理に対する思いや考えなどをすべて記しました。
8000語オーバーという, 私のブログでも類を見ない超大作になりましたが, ぜひ最後まで読んでみてください!
目次
筆者は何者か
まず記事を書く前に、私が一体何者なのかを紹介しましょう。
私は北大医学部に通うごく普通の医学生です。
しかし、現役の頃から物理が振るわず、大の苦手科目でした。
そこで、浪人の夏休みまるごと使って、いわゆる「微積物理」を主軸に物理を学習しました。
結果、物理を英語に次ぐ得意科目レベルまで持っていくことができました。
第1回名大オープン↓
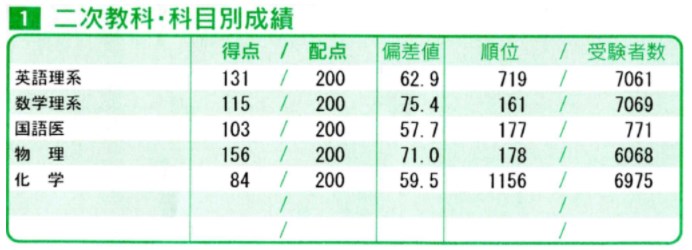
第2回名大オープン↓
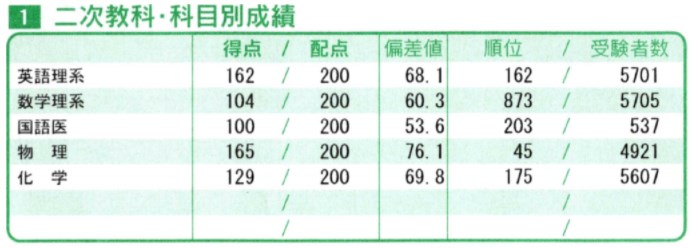
見ての通り, 二回目の名大オープンでは8割オーバー, 全国40位という驚異的な伸びを見せました。
微積物理を学び, 物理が好きになったおかげだと思っています。
「微積物理」という言葉に対する私の本音
微積物理とは?
まず、微積物理とは何なのでしょうか?
簡単に説明すると、
高校物理を本来用いることが推奨されていない微積を用いて理解していこう
というものです。
物理選択の人なら知っているかもしれませんが、簡単な例では
変位を微分すれば速度、速度を微分すれば加速度
といったものがありますね。
「微積物理」なんて単語があるのがおかしい
いきなりテーマを否定する形になってしまいますが、見出しのとおりです。
そもそも”微積物理”なんていう単語があるのがおかしい
と、私は思っています。
物理のあらゆる法則は微積をもとに成り立っています。
微積物理という単語はなんだか「頭痛が痛い」「海底の底」
と似たようなものを感じさせます(´ー`)
大人の事情: 高校物理では微積を使わないようにしている
しかし、日本の高校物理では絶対に微積を使わなくても解けるように教えられます。
また、入試問題においても同様です。
どんな問題であっても、微積を使わずに解けるようになってます。(絶対に)
微積を使わないと解けない問題はまずありません。
物理は微積をもとに成り立っているので、なんだか変な気もしますが(^^;
とにかく、高校物理では基本的に微積は使うことはないです。
このような背景があるからこそ、微積物理という単語が存在する理由になっているんですね(´-ω-`)
微積物理は念能力
HUNTER×HUNTERをご存知でしょうか?
知らない人はすみません(>人<;)
HUNTER×HUNTERでは念能力という、一定のレベル以上のハンターが使いこなしている能力がありますよね。
微積物理はまさにそれと一緒です。
こう考えてください。
- 微積物理↔念能力
- 入試↔ハンター試験
受験生は入試という、いわばハンター試験のようなものを受けます。
そのハンター試験では、念能力を習得していることを前提としていません。
すなわち、
念能力を使えなくてもハンター試験は合格できる
ということです。
しかし、ハンター試験受験者の中には念能力をすでに使える人もいますね。
ヒソカとかイルミとか…(´-ω-`)
もちろん、ハンター試験では彼らは敵なしでした。
いま、これを入試に置き換えてみてください。
微積物理は念能力みたいなものです。
使いこなせば、もちろん入学試験では無双できるでしょう。
ハンター試験で念能力を使うのは反則ではないのと同様、
実際の入試でも微積物理を使って解いても問題はないと思います。
ただ、念能力同様、習得には非常に時間がかかるし、付け焼き刃で習得してもかえって足を引っ張るだけでしょう。
実際に使ってみましょう
この問題、解けますか?
説明だけではあれなんで、実際に使ってみましょう( ´ ▽ ` )ノ
この問題を考えてみましょう!!

スイッチを入れた時間をt=0として、時間tにおけるコンデンサーの電荷を求めていきましょう。
物理を習っている人なら、この問題ではコンデンサーの電流qが時間tによって変化する、
すなわち電流qは時間tの関数だということがわかると思います。
さて、その関数を今から求めていくわけです(´-ω-`)
まず、図に電流と電荷、電圧降下を書いていきましょう(`・ω・´)ゞ
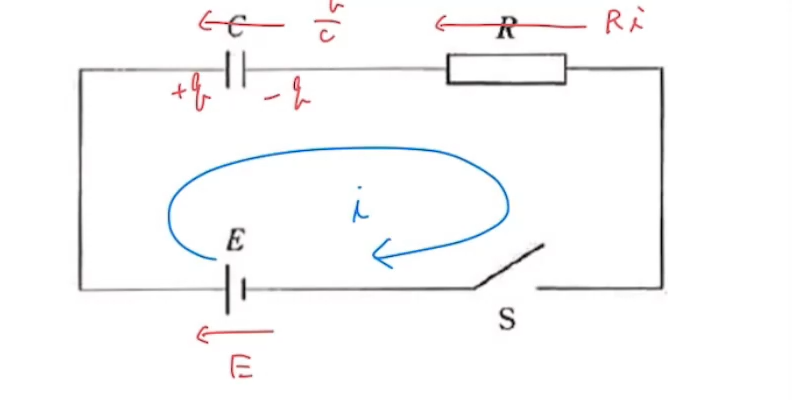
(上の方ちょっと切れちゃいました。ごめんなさい。)
次に回路の方程式(キルヒホッフの第2法則)より、次の式が成り立ちます。

ここまでは別に高校物理でもやる内容だと思います。
しかし、このままだと電荷qを時間tの関数として求めることは出来ませんね。
ここから微分要素が出てきますよ( ˘ω˘ )
電流の定義って?
まず、電流の定義は何でしょうか?
電流とは「電荷の時間変化」ですね。
これを式で表すとこうなります。
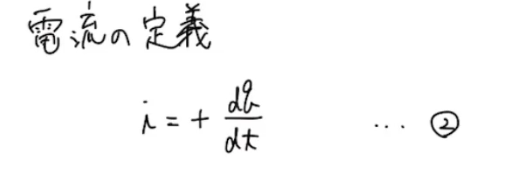
そして、この②を①に代入すると、こうなります!!
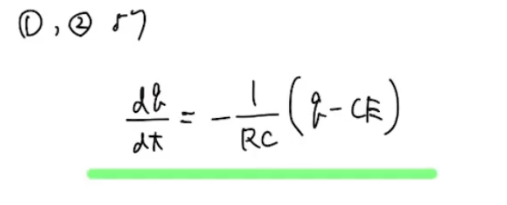
全体の流れはこんなかんじになってます。
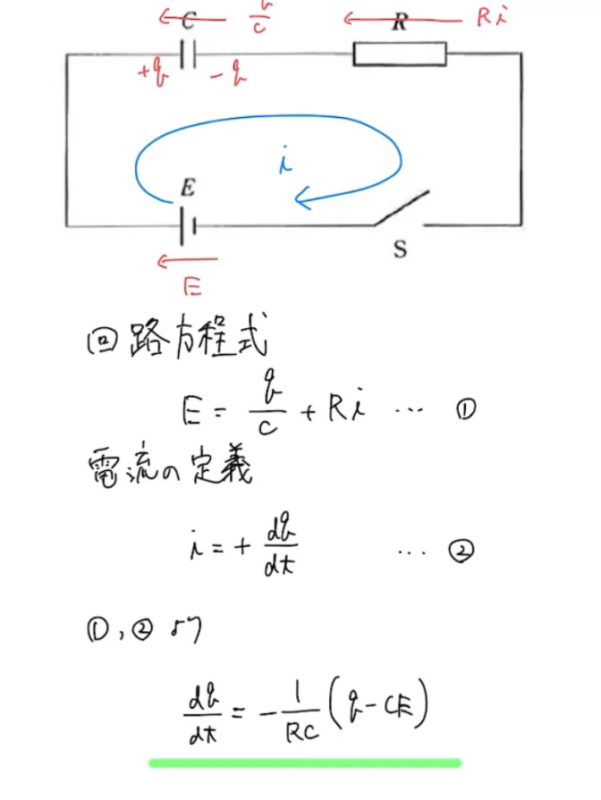
なにやら訳のわからん式が出てきましたね(´-ω-`)
まだまだこれからですよ( ˘ω˘ )
微分方程式を解く!!
今こんな式が出ました。
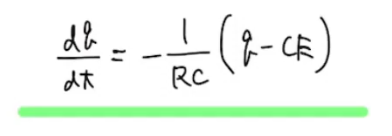
さて、この式をみてピンと来る人もいるかも知れませんね。
そう、これは数3のチャート式などにも載っている、
「変数分離型の微分方程式」
です!!
これを解くと、
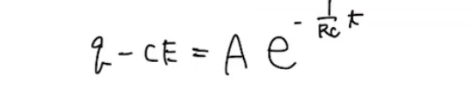
こうなります。
電荷qを時間tの関数で求める事ができましたね。
Aは任意の定数です。この定数は初期条件で決まります。
もちろんAの値も求めることも出来ます。
初期条件をこの式に代入すればいいんです。
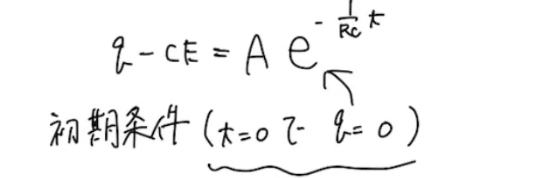
初期条件を代入すると…
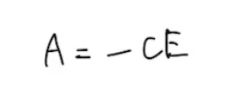
はい、Aを求められましたね(´-ω-`)
さて、このAを代入すると
電荷qを時間tの関数で表すことが出来ました!!!

これで問題は一応解けました。
数式だけではイメージしにくいと思うので、グラフにしてみました。

図はかなりアバウトです笑
よく教科書で見る図が描けましたね。
実はこれ、実際の入試問題です。
なんでこんな問題を例に上げたかといいますと、
この問題が実際に入試問題に出題されたからです。
昭和大学医学部の一次試験に出題され、私もこの問題を本番で解きました。
もちろん、誘導が用意されていて微積を使わずとも解ける問題になっていました。
しかし、
その誘導はかなりややこしかったのを覚えています。
私は本番でその誘導にうまく乗れず、全くわからなかったのです。
そこで最終手段で上でやったように
微分方程式を立てることによって、なんとか解くことが出来ました(´-ω-`)
このように、微積を使うことによって半分裏技的に入試問題を解くことが出来ます。
また、この問題に限らず、入試問題で微積分が背景になっている例はかなり多いです。
なぜ微積物理を学ぶのか
以上、微積物理についてざっくりとした解説をしました。
では、なぜその微積物理を学ぶのかを解説していきましょう。
入試問題の背景が理解できる
微積物理のメリットは、先程例で示したように
入試問題の背景を理解できる
ということが大きいと思います。
入試問題を俯瞰できるということです。
皆さん, こんな経験はありませんか?
とりあえずゴチャゴチャした誘導に乗って, 20個目くらいの穴埋めで意味不明な式が完成して, そこにtを代入したらなんか答えが出た…
これは本質を理解していないから起こる現象で, しっかり本質から学んでいる人は
「ああ, おれは典型的な重心系の問題だな」
「ここの電位は時間tの関数で二次関数的に変化するから…」
というふうに, 問題の背景を理解しながら解くことができます
背景がわかっているとわかっていないとでは, こと難関大などでは特に差がつくと思います。
公式を導出できる。意味がわかる。
- ポアソンの式はなぜ中途半端な5/3乗といった数字が出てくるのか?
- 万有引力のポテンシャルエナジーのようなややこしい式はどこから出てきているのか?
微積で物理を学べばこれらを理解することができます。
こういったことが理解できるようになるのも、微積で高校物理を学ぶメリットの一つですね。
定量的な視点が身につく
定量的な視点とは、
「物事の様子や変化を数式で捉える視点」
のことです。
定性的が反対の意味です。
これだけ見てもパッと来ないと思いますが、先程の入試問題の例を思い出してください。
高校物理では、
この図とともに、

「コンデンサの電荷は最初は早いペースで溜まり、だんだん溜まるペースが落ちていく。」
と教わると思います。
これが定性的な視点です。
一方、微分方程式でこのような式を求めました。

この式によって、先程のグラフの形が数式で理解できます。
これが定量的な視点です。
このように、高校物理で習う定性的視点に加え、微積物理による定量的な視点を身につけることができます。
物理を好きになれる。楽しいと思える。
微積物理を学ぶ一番のメリットは, やっぱりこれ。
物理が嫌いで苦手だった私でしたが、微積物理を学んだ後は世界が変わりました。
無味乾燥な公式暗記、典型問題暗記から解放されました。
まず、運動方程式を立てて物理現象を観察する。
その式が数式として解けるか吟味してみる…
物理を心から楽しむことができました。
あんなに嫌いだったのに、いろんな解き方がないか研究したり、微積で解き直してみたり、
物理を楽しいと思えるようになりました。
。。。
これだけ見るといいとこだらけだと思いますが、もちろんデメリットもあります。
微積物理は圧倒的に遠回りな道のり
デメリットはなんと言っても
習得が大変
ということです。
高校物理を十分に理解した上で、もう一度イチから物理体系を習得していかなければなりません。
おそらく使いこなせるまでには少なくとも1年はかかるでしょう。
私の場合、高3の夏から微積物理を始めて、一浪の夏にやっと使えるレベルにまでなりました。
さらに、私のように高校物理の内容も曖昧なまま微積物理を学ぶのは圧倒的に非効率です。
私の場合、
普通に高校物理を学ぶよりもかえって遠回りになった
という結果になってしまいました。
どんな人におすすめ??
微積物理が適しているレベル
正直、全員におすすめしたいですが…(´-ω-`)
私のように、微積物理を学んだことによって、かえって遠回りになってしまうのは避けたいですね。
よって、少なくとも高校物理レベルならある程度基礎から理解できていることが望ましいです。
また、習得に時間がかかることから、あまり時間が残されていない人にはお勧めできません。
高3で十分時間があり、物理が得意で得点源にしたい人にお勧めです。
志望校
とくに、ハイレベルな大学になってくると、微積が背景となっている問題が多くなっています。
ここで言うハイレベルな大学とは、東大・京大・東工大など、超ハイレベルな理系科目難易度が高い大学群を指します。
私の通っている北大医学部レベルでも、微積物理は必要ないです。
北大レベルなら明らかにオーバーワークです。
本当に最高難度の大学を受ける方には、微積で物理を学ぶ必要はあるのかなと思います。
また、そういった大学を受験する人は微積物理を学んでいる人が多いです。
可能性は低いですが、微積物理を学んでないことで不利になってしまうこともあるかもしれません。
微積物理に対して思っていること
微積物理という単語は、マジで謎。
改めていいますが、私はこの「微積物理」という単語が嫌いです。
ここまで記事を読んでくれた方はわかったはずです。
物理と微積は切っても切り離せないもの。
なのに、微積物理という単語で微積を使った物理へのアプローチが特別視されているのは納得がいきません。
正直、これがいいたくてこの記事を書いたと言っても過言ではありません笑
高校物理も大事
微積物理を学んでいる人が高校物理をバカにしたり、逆に、微積物理を必要以上に嫌ったりする。
こういったケースを目にすることがあります。
もちろんどっちも良いものとは言えません。
微積物理の定量的な視点はもちろん重要です。
ですが、高校物理で習う定性的な視点も同じくらい重要です。
どちらが優れているとかそういった議論はナンセンスです。
微積物理はどこで学べる?
人に教わる(おすすめ)
おそらくこちらが圧倒的にお勧めです。
微積物理は内容がヘビーなので、一人でやっていると常人は心が折れます。
私の知る限りでは
- 東進の映像授業
- 駿台のコース
- 河合塾のコース
で受けることができるみたいです。
私は東進の映像授業で受けましたが、友人は河合塾で対面授業で教わっていました。
独学する(難易度高め)
微積物理を独学するのはかなりの根性が要りますが、それでもいけるというど根性タイプの人なら独学も選択肢としてありですね。
お勧めの教科書は
- 新物理入門
- 親切な物理
ですね。
新物理入門
私も持っていますが、正直大学生になった今読見返しても結構難しいです。
大学の一般教養科目でも物理の講義はありますが、それよりも高度な内容でした。
入門とタイトルにありますが、かなりハイレベルな内容を扱っています。
数学的要素が多く、数3の実力もないとかなりしんどいでしょう。
ですが、高校生向けの微積物理の本ではもっとも詳しく解説がのっていると思います。
また、新物理入門の問題集もあります。
こちらもなかなか難易度が高く、解説も微積をバリバリに使ってます(´-ω-`)
微積物理を使いこなす練習をするにはぴったりです。
新物理入門は駿台出版の本ですが、河合塾にも微積物理の本もあります。
理論物理の道標という本です。
書店で読んでみましたが、こちらもかなりヘビーな内容でした。
使うならどちらかで大丈夫でしょう。
親切な物理
こちらは親切な物理という本になってます。
タイトル通りかなり丁寧な解説がされており、
理解が難しかった束縛条件の理解の補助になりました。
1950年代からのベストセラーだそうです(´-ω-`)
絶版になったものの、復刻版が出版されたみたいですね。
公式導出なども微積を用いた解説になってます。
ただ、上巻と下巻の2部構成となっています。
かなりゴツくて重厚です(´-ω-`)
微積物理の参考書まとめた記事も書きました!!
ぜひそちらも合わせてご覧ください!!
微積物理の勉強方法など
ここに書くと長くなるので、他の記事に詳細に書くことにします。
勉強法以外にも、私自身の習得エピソードも書く予定です!
ぜひ参考にしてみてください( ・∇・)
追記:書きました
いちばん大事なこと: 微積物理を学ぶ意味って何?
微積物理は念能力だ, なんて表現もしましたが, ここで一つ言っておきたい。
微積物理は魔法でもなんでもないってこと。
微積物理をマスターしたらどんな受験物理の問題が来ても怖くない。無敵だ。
なんて勘違いをしている方が散見されます。
というか, 微積物理を学ぶ前の私もそうでした。
受験物理が微積を用いなくても解けるようになっている以上, 微積物理なんて遠回りな手段を取らなくても受験に合格することが十分可能です。
というかむしろ, 微積物理に中途半端に時間をかけて演習・アウトプットが疎かになり, 逆に点数が取れなくなる, なんてこともよくあります。初期段階は特に。
もちろん, 微積物理を学ぶことで定量的な視点が身につき, 問題を俯瞰することもできるようになるとは思います。
しかしながら!!!
一部の超超超難関(東大京大東工大)を除いては, 微積物理を学ぶことで有利に解けたりする問題などほとんどありません。
それは, 現状の受験物理は「典型問題の高速処理」「厳しい時間制約」という条件のもとに作られているからです。
これがもし, 超本質的な問題でかつ, 時間もたっぷりあるなら話は別です。
しかし, 現実は違います。
何度も言いますが, 別に微積物理を学ばなくても, 典型問題集を周回して高速で解けるようにすれば, 北大の二次試験くらいなら余裕で満点近く取れます。
つまり, 微積物理はあえて悪く言うならば,
「習得にかかるコストにしては, そこまで試験で優位に出られるわけでもない」
というなんとも微妙な立ち位置です。
では, なぜ, 微積物理を学ぶのか???
それは, 物理を心から好きになるためだと思います。
私自身, 物理という科目が大の苦手でマジで嫌いでした。
高校の授業では課題もろくにやらず, テストで20点とか普通に取ってました。(100点満点です)
そんな私でしたが, 浪人の夏休みに覚悟を決めて, 一ヶ月すべてを物理に捧げ, 微積物理を学びました。
今までは物理という科目は,
とりあえず典型パターンを見つけて, この公式を当てはめて…
みたいな, 一種のパターン学習程度に思っていませんでした。
しかし, 微積物理で物理を本質から学び直すことで, 問題を解くときも
「なるほど, 力がこう加わっているから運動方程式はこうなって, 運動自体はこういう関数で表せるんだ!!」
という感動を毎回味わうことができるようになりました。
それが楽しくて仕方がなかった私は, あらゆる模試や大学の過去問を解きあさり, 解法研究をたくさん行いました。
「物理っておもしろい!!!!」
そうして物理の問題を解き漁っているうちに, いつの間にか, 物理が得意になっていたという具合です。
「好きこそものの上手なれ」
という言葉がありますね。全くそのとおりだと思います。
少し個人的な話になってしまいましたが, もう本当にこれは好みの問題です。
自分がどうしたいかで選んでください。
「いや, 別におれはそんなことしなくても物理の点数は安定してるからいいや」
という人は, マジで必要ないと思います。まぁ大学に入ってからやるし。
一方で, 私のように「物理ってマジでパターンゲーで面白くないなぁ」という思いを抱いている方には, 微積物理を学んで見る勝ちはあるのかなぁと思います。
何度も言いますが, 微積物理の習得は超超超大変ですし, そこまでメリットも多くないです。
それでも, 学んでやろう, 物理という学問を楽しみたいという方
ぜひ, 一度本を手にとって, あるいは予備校の授業を受けてみることをおすすめします。
前述したように, 習得にかかる手間や時間の割には, そこまで試験で圧倒できたりするわけではありません。
コスパは非常に悪いです。
しかし, それは「物理を受験の点取りゲームの科目としか見てない狭い視点」における話なんですよね。
受験生の皆さん, 物理を一つの体系的な美しい学問として学んでみませんか?
物理のあらゆる現象には, 理路整然とした数学的事象が絡んでいることを発見して, 感動を味わいませんか?
ということで, 私がこの記事で伝えたいことはすべてかけたと思います。
これを読んで, 微積物理を学んでみるもよし, やっぱやめとこって思うのもいいと思います。そこは個人の自由です。
そして, 微積物理を学んでやろうという「物理オタク」の方, またはその予備群の方
さぁ, 思う存分, 物理という学問を楽しんでください!!!!








