こんにちは。
悩める医学生、しらいです。
私は微積物理という単語は嫌いなのですが、今回はそういった
微分積分を高校物理に取り入れて勉強している方
に向けた記事となっております。
私自身、微積は頻繁に高校物理で使用してきましたが、その中で色々なミスを犯してきました。
この記事ではそういったミスをまとめました。これから勉強する方の参考になれば幸いです。
また, 他の記事では私の微積物理に関する考え, 意見などを書き尽くしているので, そちらも御覧ください。
目次
1. 圧倒的な演習不足
私の体験談
微分積分を使って物理を理解するのは高校の範囲を遥かに逸脱しているため、理解に時間を要します。
具体的に何をするのかは上に貼った記事を参照してもらいたいのですが、公式などの導出や微積を使った定量的な解法をメインに学んでいきます。
よって、高校物理をガチガチにやっている人には不慣れな部分が多く、インプットにとてつもない時間がかかるのです。
私の場合、
- 力学:50時間
- 波動:30時間
- 電磁気:50時間
- 熱力学:20時間
合計170時間くらいをインプットのためだけに割きました。
浪人の夏休みの半分くらいの勉強時間は物理のために割いたと思います。
こんだけやったんだ。
単振動、円運動などの運動方程式の解も出せる。
エネルギー積分も導出できる。
回路方程式から時定数を微分方程式を解いて導出できる。
マクスウェルの方程式から電磁場の諸公式を瞬時に導ける。
私は無敵だ。
高校物理において敵はない。
そう思い込んでいざ入試問題と対峙しました。
するとあら不思議。
全く解けなかったのです。
いや、入試問題はおろか、名門の森のような典型問題も全然解けない…
公式の導出や、高校の範囲を逸脱した定理の理解などはほぼ完璧に覚えていました。
でも解けない!!
このとき気が付きました。
インプットしても問題が解けるようになるわけじゃない
ということにです。
考えてみれば当たり前ですよね。
いくら数学の教科書を読んでも問題が解けないのと一緒です。
いくら微積で物理を理解したところで、それを使って問題を解かないとなんの意味もありません。
インプットに時間を欠けすぎるくらいなら、微積なんて使わずに問題集をひたすら解いていたほうがマシです。
こちらの記事も是非参考にしてみてください。
よって、微積を学んでいる人は特に、ただでさえ発展的で不慣れな微積を用いた解法を自分の道具にするために、
インプットよりも同じくらい大量にアウトプット、つまり問題演習をするべきです。
演習量にまさるものはないです。
大学の物理を少し齧ってイキってる痛い受験生にならないようにしましょうね。
こういうわけで、微積をつかって高校物理を理解するのが難しく、大量の時間を要するのです。
問題演習に使える教材
殆どの教材は微積など用いずに問題解説をしています。
これは文部省がそう定めているからです。「高校物理では一切微積を使うな」と。
よって、微積を使った解法を身につけるためには、やや発展的な問題集で演習を行う必要があります。
以下、私がおすすめする問題集を紹介します。
新・物理入門問題演習
言わずとしれた物理の最高難度問題集です。
問題一つ一つに骨があり、解説も微分積分を多用しています。
力学では束縛条件、エネルギー積分、運動方程式の解き方など…
電磁気では回路方程式の解法など…
微積をベースの解法がほとんどです。
逆に微積の解法を使いたくてたまらない人にはこの本はバイブル的存在になるでしょう。
また、記述問題解説もあり、入試の記述答案の書き方の参考になります。
微積を使った解法を学びたいなら私は間違いなくこれをおすすめします。
これをマスターした暁にはほとんどの入試問題は手を取るようにわかるでしょう。
一般的な典型問題集
忘れてはいけないのが、基礎的な典型問題集です。
典型的な問題集とは「名門の森」といった、標準レベルの大学向けの問題集になります。
普通の受験生ならこれを完璧になるまでマスターしてきます。
パターン化や解法暗記は百害あって一利なし。
とはいえど、やはりこういった標準問題も解けるようにしておくべきです。
微積を使って学んでいる方に是非オススメしたいのは
微積不使用、使用の両方の解法で解けるようにしておく
ことです。
高校物理の定性的視点と大学物理の定量的視点のつながりを意識することができます。
よって、典型問題集に加え、プラスαで新物理入門のような発展的な問題集をやるのが理想です。
2.公式の暗記を怠る
微分積分で物理を学んでいると陥りやすいミスの2つ目は、
公式暗記を怠ることです。
微積を使って学んでいると、加速度の式や万有引力のポテンシャルエネルギーなどといった、
丸暗記系の公式を覚えることに疑念が湧くでしょう。
微積を使ったらこんなのすぐ導出できるのに、なんで導出をごまかして暗記させようとするんだ…
これも文部省がそう定めているので仕方がありません。
高校物理の教科書では少なくとも微積は使わずに導出がされるように記述されているはずです。
よって、微積ユーザーはこのような考えに囚われます。
無味乾燥な丸暗記<<<導出する過程

よって、公式暗記=悪のようなイメージを持ってしまうのです。
もちろん、導出できるのは大事ですし、まっとうなことを言っています。
しかし、肝心の公式を覚えないのは、公式を理解したことにはなりません!!
公式を理解している=「公式の意味(導出過程とか)を理解している」かつ「公式を暗記している」
という状態であることを念頭に学習してください。
試験中に
「万有引力のポテンシャルエネルギーってなんだっけー、まぁ導出すればいいか…」
なんて時間はありません。
基本的にどの大学も物理は制限時間がかなり厳しいです。
よって、公式は導出を理解するのも大事ですが、暗記することも必要だということを肝に銘じておいてください。
そもそも理解してない
字面を追ってるだけ状態

上の画像は私が実際に使っていた物理のノートのほんの一部です。
このように微積を使って勉強していると、必ず数式の羅列に遭遇します。
そういった数式をこねくりまわして定理や公式を導出するのです。
しかし、これもよくあるミスなのですが、
なんとなく式の字面だけ追って理解したつもりになっている
状態もよく見受けられます。
これは数学などにも言えると思いますが、解説を読んで理解したつもりでも、いざ問題を解こうとすると手が動かない
といった例です。
対処法
私が実際にやっていた勉強法を紹介します。
まず、白紙を一枚用意してください。
そして、学習した項目、例えば「エネルギー積分」だったら
運動方程式からエネルギー保存則を導出する流れを白い紙にイチから自力で再現してみてください。
例えばこんな感じです。

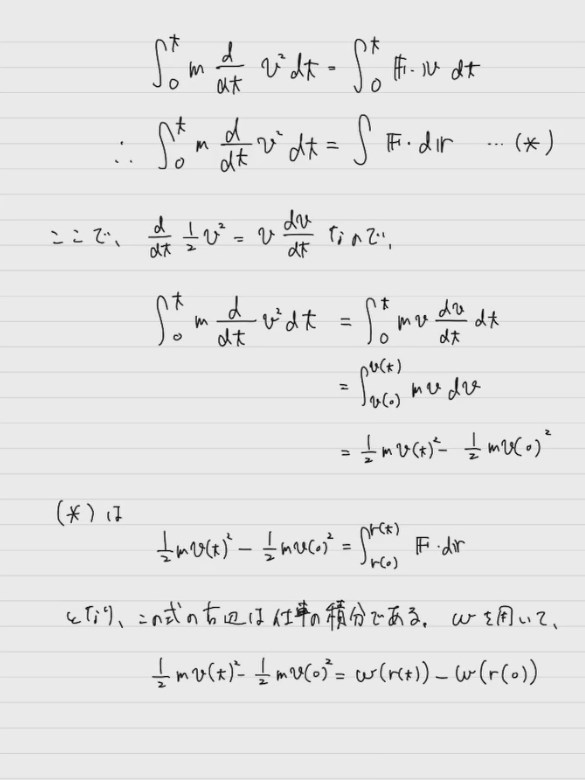

もし、何も見ずにこの流れを導出できたら、あなたはエネルギー積分を理解していると言えるでしょう。
それができなかった場合はまだ理解が足りていません。
こういった感じで自分の理解度をチェックすることができます。
この勉強法、物理以外にもなんでも使えるので本当におすすめします。
有名なあのセリフ
「数式は言葉だ…計算じゃない。」
かの有名な某予備校講師のセリフですね。
今になって、この意味がよくわかります。
何がいいたいか?
みなさん、以下の式を見てください。
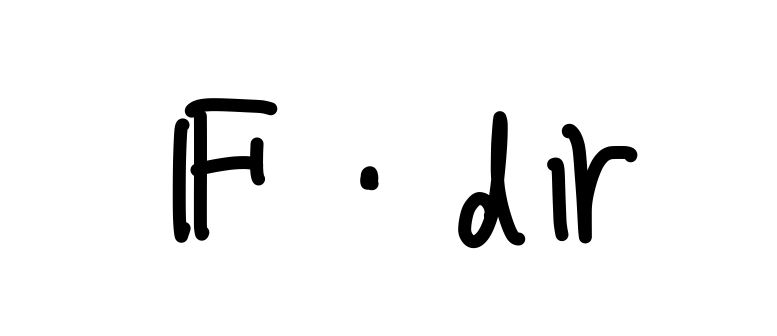
これを見て意味が理解できましたか?
Fかけるdr?
なんて思った方、全然理解が足りてませんよ。
これをみて、
あ、これはFベクトルと微小変位drの射影の掛け算(スカラー積)だなと、瞬時に意味として理解し、さらに下の図まで想像できたのなら合格です。

微積を使って物理を理解しようとすると、こういった不慣れな数式を理解していかなければなりません。
このように、数式を言語のように理解していくことが鍵になります。
これは物理に限った話ではないのですが、普段から数式をなんとなく目で追うのではなく、「意味」を理解するよう心がけてください。
4.発展的な内容ばかりに時間を使う
浪人の夏休み一週間を奪ったマクスウェルの方程式
今でも記憶に残っているのが、
微積物理を浪人の夏休みに勉強していたとき、「マクスウェルの方程式」という物理の超有名な法則があるのですが
それを理解するのに1週間かけたことですね。
↓マクスウェルの方程式
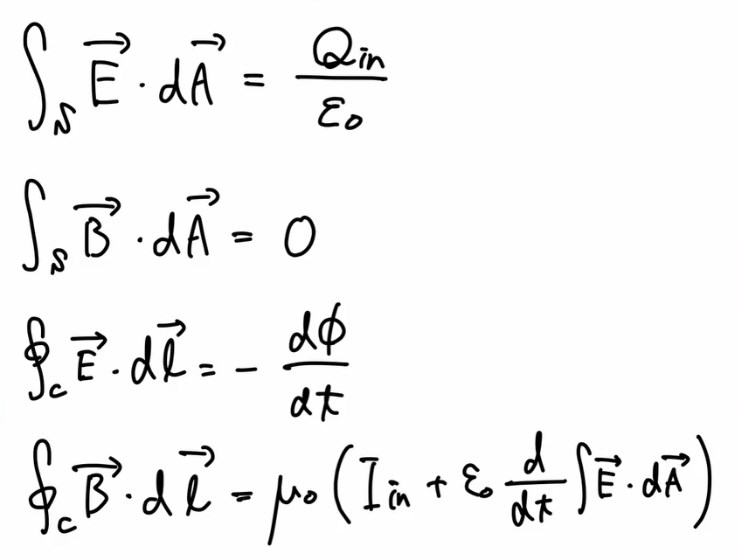
ちなみにこの公式から電流周りの磁場の大きさとか、コイル内の磁場の大きさの公式を導出することができます。
私は大学生でも理解に苦労するような内容を、よりによって浪人の夏休みに取り組みました。
線積分やらなにやらわけのわからない大学数学の知識を使い、何度も講義録を見直しました。
そして貴重な1週間を溶かした結果、ビオ・サバールの法則から電流周りの磁場の大きさを求めることができるようになりました。
。。。
いくらなんでもオーバーワークすぎる…
殆どの受験生が10分で理解(暗記)できるような内容に1週間も使ってしまうなんて。
あの頃の私は異常なまでに微積物理信者だったので、そんなことすら気にかかりませんでしたが。
今思えばもっと有効な時間の使い方があったのかもなぁと思ってます。
結果、そのビオ・サバールなんちゃらは受験の役に立ったのか。
はい、一切役に立っておりません笑
やって無駄とはいいません。
でも、受験には使わないということだけは言っておきます。
しかし、それが役に立つ瞬間が一度だけありました。
それは私が受験を終えてから半年以上経ったとき。
物理学の電磁気学のテストで、ほぼ勉強せずに成績上位者に入ることができました
あのときの頑張りは無駄ではなかったんだね…涙
とはいっても、物理を微積で考えるのって本当に楽しいです。本当に。
私も微積を使って学んだおかげで、物理が好きになったし得意科目になりました。
物理の一見意味不明な公式を、当たり前のような定理から導けるあの快感。
本当にロマンです。
大事なのはバランスです。
物理を学ぶ上で良いモチベーションにもなります。
せっかく微積を使って学ぶんです。
発展的な内容にも臆せずにチャレンジしてみてください。
そして、どうしてもわからないことがあれば、大学入学後のお楽しみとして、しばらく寝かせておくのがいいと思います。
特に電磁気の分野を微積で勉強する方は覚悟しておきましょう笑
おわりに
今回は微積を使って物理を学ぶ人へが陥りやすいミスを紹介しました。
微積を使って理解するのは、多少は遠回りになることは自覚しておきましょう。
もはや”趣味”の領域です。
しかし、微積を使って学ぶと必ず物理が好きになります。
大学受験に毒された無味乾燥な丸暗記や理解の伴わないパターン化ではなく、もっと有意義な勉強への姿勢が身につきます。
大学受験のための間に合わせのような学問ではなく、人生をより豊かにするための教養として、物理を学ぶようになっていることでしょう。
ですので、時間がある方はぜひ、微積を使って物理を学んでみてください。
健闘を祈ります!!
それでは!!( ´ ▽ ` )ノ




